[TOC]
数据是什么
转载地址: https:/blog.csdn.net/u013164931/article/details/80189351

数据: 是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识别,并输入给计算机处理的符号集合。其实就是图书馆中所有的书。
数据元素: 是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理。也被称为记录。就是书。
数据项: 一个数据元素可以由若干个数据项组成。其实就是书名、作者、出版社啥的….
数据对象: 是性质相同的数据元素的集合,是数据的子集。其实就是某一类书。
**数据结构: **(data structure)是数据的组织形式,数据元素之间存在的一种或多种特定关系的数据元素集合。
数据类型: 是按照数据值的不同进行划分的可操作性。在C语言中还可以分为原子类型和结构类型。原字类型是不可以再分解的基本类型,包括整型、实型、字符型等。结构类型是由若干个类型组合而成,是可以再分解的。
什么是结构
转载地址: https:/blog.csdn.net/u013164931/article/details/80189351
分为 逻辑结构、存储(物理)结构。
逻辑结构
概述
是指数据对象中数据元素之间的相互关系。这里也就表示书和书的关系。 包括集合结构、线性结构、树形结构、图形结构。
**集合结构:**集合结构中的数据元素除了同属于一个集合外,它们之间没有其它关系。
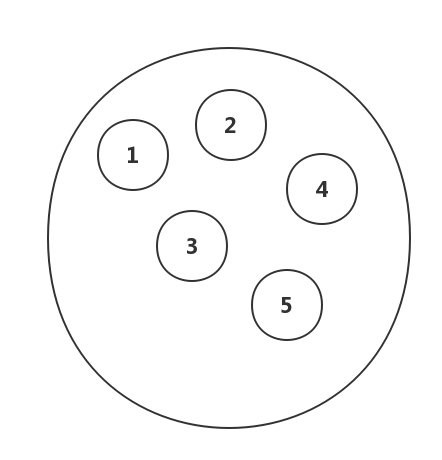
线性结构: 线性结构中的数据之间是一对一的关系,并且是一种先后的次序,就像a-b-c-d-e-f-g·····被一根线穿连起来。
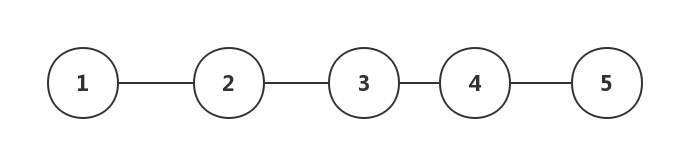
**树形结构:**树形结构中的数据之间存在一种一对多的层次关系。
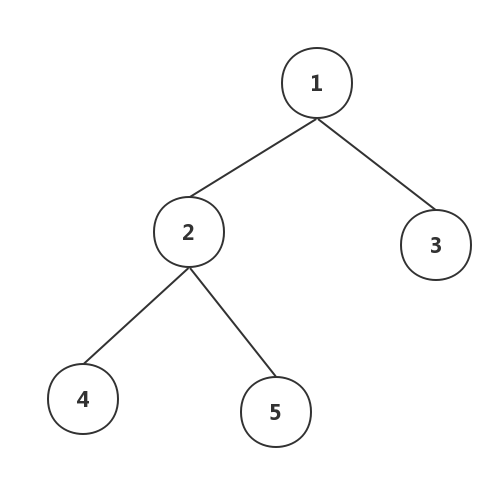
**图形结构:**图形结构的数据元素是多对多的关系。
存储(物理)结构
概述
存储结构(storage structure)也称为物理结构(physical structure),指的是数据的逻辑结构在计算机中的存储形式。数据的存储结构一般可以反映数据元素之间的逻辑关系。分为顺序存储结构和链式存储结构。
**顺序存储:**是把数据元素存放在地址连续的存储单元里,其数据元素间的逻辑关系和物理关系是一致的。
链式存储:是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的,数据元素的存储关系并不能反映其逻辑关系,因此需要借助指针来表示数据元素之间的逻辑关系。
总结
数据的逻辑结构和物理结构是密切相关的,在学习数据的过程中会发现,任何一个算法的设计取决于选定的数据逻辑结构,而算法的实现依赖于所采用的存储结构
什么是算法
原文链接:https:/blog.csdn.net/csdn_aiyang/article/details/84837553
概述
还是图书馆的例子,如果一本一本找累死人,要是有个索引,先找哪一类这样会快很多。如何查找其实就是算法。
算法是解决问题步骤的有限集合,通常用某一种计算机语言进行伪码描述。通常用时间复杂度和空间复杂度来衡量算法的优劣。
程序=算法+数据结构。数据结构是算法实现的基础,算法总是要依赖某种数据结构来实现的。算法的操作对象是数据结构。区别是数据结构关注的是数据的逻辑结构、存储结构有一集基本操作,而算法更多的是关注如何在数据结构的基本上解决实际问题。算法是编程思想,数据结构则是这些思想的基础。
时间复杂度
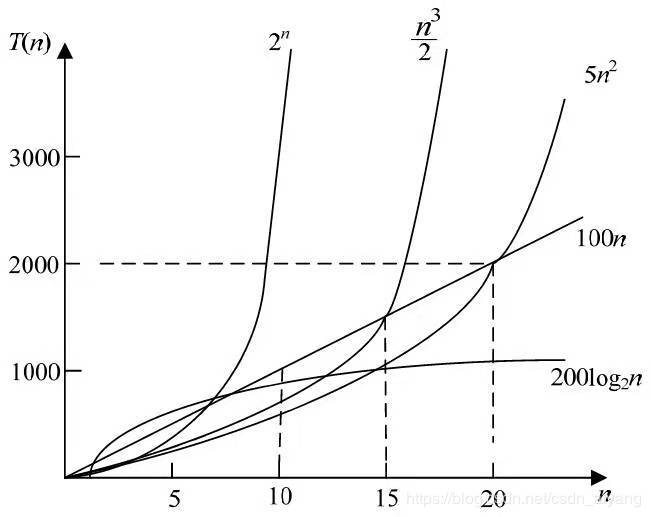
在进行算法分析时,语句总是执行次数 T(n) 是关于问题规模 n 的函数。进而分析次数T(n)随规模n的变化情况并确定T(n)的数量级。算法的时间复杂度就是算法的时间度量,记作T(n) = O(f(n))。它表示随问题规模n的增大,算法的执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度。其中,f(n)是问题规模n的某个函数。
算法的时间复杂度是衡量一个算法好坏的重要指标。一般情况下,随着规模n的增大,次数T(n)的增长较慢的算法为最优算法。常见时间复杂度从小到大依次排列:O(1) < O(log2n) < O(n) < O(n²)<O(n³) ····<O(n!)
空间复杂度
空间复杂度(space complexity)作为算法所需存储空间的量度,记做S(n) = O (f(n))。其中,n为问题的规模;f(n)为语句关于n的所占存储空间的函数。
一般情况下,一个程序在机器上运行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单位。若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常量,则称此算法为原地工作,空间复杂度为O(1)。
什么是数据结构
转载地址:https:/blog.csdn.net/csdn_aiyang/article/details/84837553
概述
是指相互之间存在一种或多种特定关系的数据元素的集合用计算机存储、组织数据的方式。数据结构分别为逻辑结构、(存储)物理结构和数据的运算三个部分。
数据结构的主要任务是通过分析数据对象的结构特征,包括逻辑结构及数据对象之间的关系,然后把逻辑结构表示成计算机课实现的物理结构,从而便于计算机处理。
常用数据结构
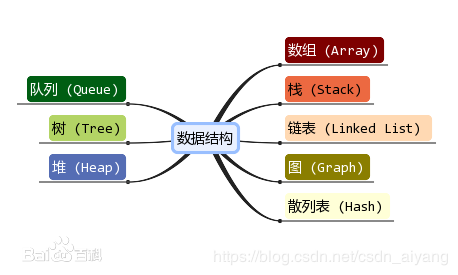
红框里的内容就是线性表的大家族了。
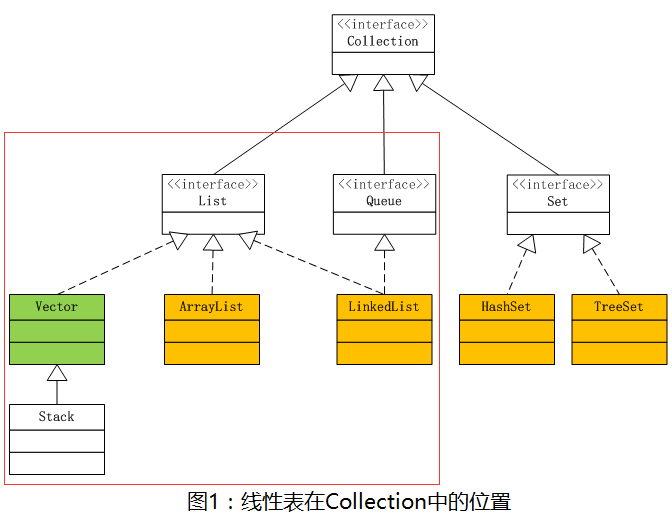
线性表
转载地址: https:/blog.csdn.net/weixin_44270248/article/details/89365754
概述
线性表是其组成元素间具有线性关系的一种线性结构,是由n个数据类型相同的元素构成的有限序列。其具有“一对一”的逻辑关系,与位置有关,除了头尾元素之外,每一个元素都有唯一的前驱元素和后继元素,即元素ai前面的元素为ai-1,后面的元素为ai+1。
线性表是由零个或多个具有相同特性的数据元素组成的有限序列,是最基本且常用的一种线性结构(链表,数组,栈,队列都是线性结构),同时也是其他数据结构的基础。
线性表的存储结构和实现
顺序存储结构——顺序表
概述
线性表的顺序存储结构,是把线性表中的所有元素按照其逻辑顺序,依次存储到计算机在内存中指定的一块连续存储空间中,成为顺序表。
元素在内存中的物理存储位置和他们在线性表中的逻辑位置一致。
特点
- 在线性表中逻辑上相邻的元素在物理存储位置上也相邻;
- 可按照数据元素的索引号进行随机存取,时间复杂度为O(1);
- 插入、删除操作需要移动大量的元素,时间复杂度为O(n);
- 需要预先分配存储空间,可能会造成空间浪费,但存储密度高,数据紧凑。
描述
常使用数组作为顺序表的底层数据结构进行存储。
总结
优点:存取元素快; 缺点:插入和删除元素慢,且需要预先分配空间,容易造成空间不足或空间浪费
顺序存储结构——链表
概述
采用链式存储结构的线性表成为链表,是用若干地址分散的存储单元存储数据元素,逻辑上相邻的数据元素在物理位置上不一定相邻,因此,链表在数据结构上分为两部分,一部分存储数据,成为数据域;一部分存储下一个元素的内存地址,成为指针域。
单链表
概述
单链表是指节点中只包含一个指针域的链表,指针域存储指向后继结点的指针。头指针为单链表的起始地址,为单链表的唯一标识。尾指针没有后继结点,其后继结点为null,可以作为单链表结束的判定标识。 为方便操作,一般会有一个头结点,头指针的数据域为空,指针域指向第一个结点,当头结点的指针域为null是位空表。

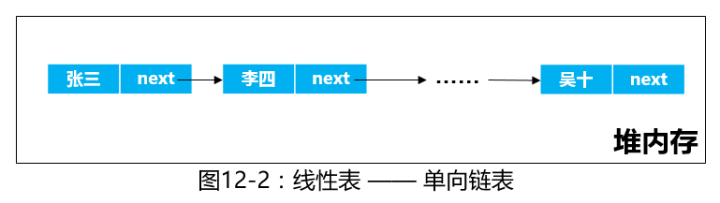
单链表结点的存储空间是在插入和删除的过程中动态生成和释放的,不需要预先分配空间,从而避免了空间分配的不足和过剩。同时,单链表在插入和删除节点时不需要移动数据,所以其插入和删除效率较高。
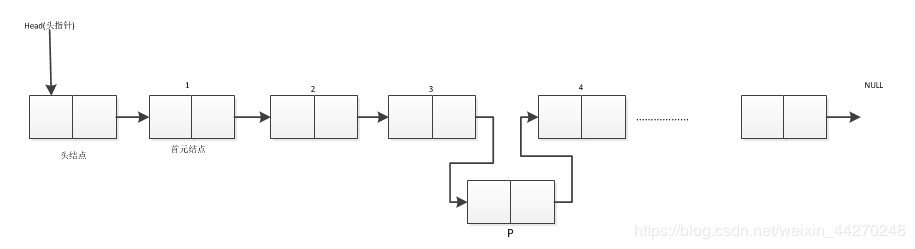
单链表类插入操作
单链表插入时,只需要找到所插入位置结点的前驱结点,然后修改前驱和新插入节点的指针域即可。
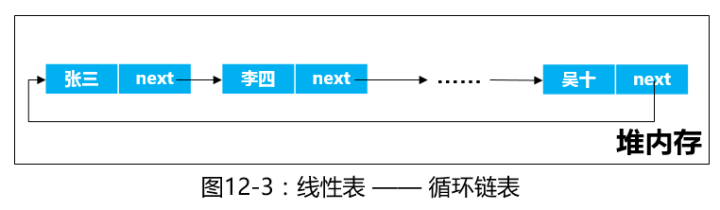
循环链表
循环链表就是在单链表的基础上修改而来,只是将尾结点的指针域指向了头结点,从而形成一个环状的链表。 在实现循环链表时可以用头指针或尾指针或两者同时使用来标识循环链表,通常使用尾指针来标识,可简化操作。 由于循环链表和单链表操作算法基本一致,所以不再赘述。
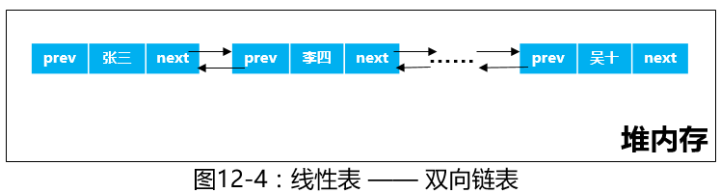
双向链表
概述
双向链表即在单链表的基础上又添加了一个指针域,用来指向其前驱结点,使得在查找某个结点的前驱结点时不再需要从表头开始顺次查找,大大减小了事件复杂度,但相应的会增加内存的空间消耗。
顺序表和链表的比较
| 顺序表 | 链表 | |
|---|---|---|
| 优点 | 1. 存储高效 2. 存储密度高,空间开销小 3. 实现简单,易于使用 | 1.灵活,可进行空间的动态分配 2. 插入、删除效率高 |
| 缺点 | 1. 需要预先分配空间; 2. 插入、删除操作时间复杂度高 | 1.存储密度低; 2. 不存在角标,查找元素时间复杂度高 |
三者的区别
1、它们都有数据域(data(p))和指针域(next(p)),但是从图中可以看出双链表有两个指针域,一个指向它的前节点,一个指向它的后节点。
2、单链表最后一个节点的指针域为空,没有后继节点;循环链表和双链表最后一个节点的指针域指向头节点,下一个结点为头节点,构成循环;
3、单链表和循环链表只可向一个方向遍历;双链表和循环链表,首节点和尾节点被连接在一起,可视为“无头无尾”;双链表可以向两个方向移动,灵活度更大。
栈和队列
转载地址:https:/blog.csdn.net/chenleixing/article/details/42392283
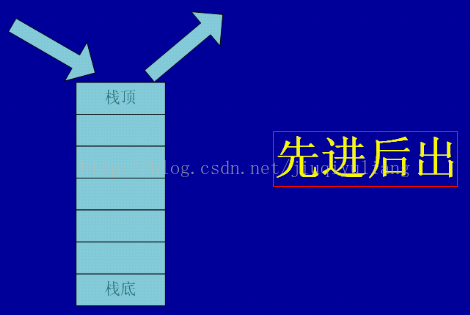
栈
基本思想:后进先出(先进后出)即栈中元素被处理时,按后进先出的顺序进行,栈又叫后进先出表(LIFO)。
队列
基本思想:先进先出即先被接收的元素将先被处理,又叫先进先出表(FIFO)。如下图所示:
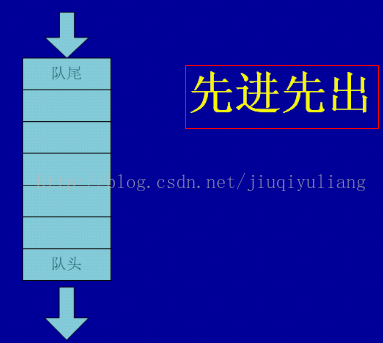
顺序队列
顺序队列的操作,要判断队满和队空的标志,从图中我们可以总结得到:
-
队空:head = tail
-
队满:tail = m
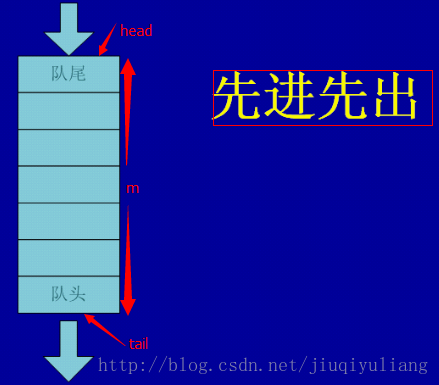
循环队列
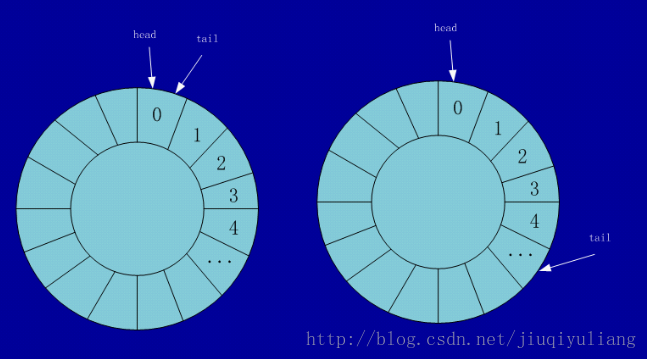
循环队列的操作,要判断队空和队满的情况,从图中我们可以总结得到:
-
队空:head = tail
-
队满:tail + 1 = head(在队列中会留一个空着的空间,所以要加1)
数组
概述
一种物理结构,它的存储单元是连续的。
数组就是相同数据类型的元素按一定顺序排列的集合。一句话:就是物理上存储在一组联系的地址上。也称为数据结构中的物理结构。
散列表(哈希表)
转载地址:https:/segmentfault.com/a/1190000018659991
概述
数组存储区间连续,查找方便,但是插入和删除效率低下;链表存储区间离散,插入删除方便,但是查找困难。大家肯定会问,有没有一种结构,既能做到查找便捷,又能做到插入删除方便呢?答案就是我们今天要跟大家说的主角:哈希表。
散列表(Hash Table)又叫做哈希表,是一种很常用的数据结构。散列表其实是基于数组实现的,可以说,没有数组就没有散列表。先来举一个简单的例子,来认识一下什么是散列表。
什么是散列表?
假如在学校的运动会上,每个运动员的胸前都会标识自己的号码,编号是1,2,3……,这样的话,我们可以很容易的将运动员信息存储在数组当中,运动员的编号就是数组的下标。但是会存在这样一种情况,假如运动员的编号不是顺序排列的,而是需要加上更多的信息,比如年级,班级,例如一个运动员的编号是15030711,15是年级,03是专业,07是班级,11是顺序号,这样的话我们该怎么存储运动员信息呢?
其实也不难,我们只需要截取运动员编号的最后两位,作为数组的下标存储在数组中,当需要根据编号查询信息的时候,我们也同样截取编号最后两位来进行查询。这就是很典型的散列思想。
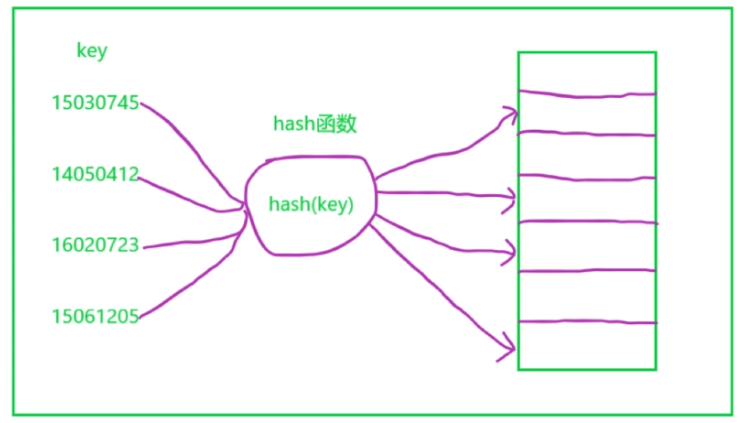
选手的编号叫做 键 , 把运动员编号转换为数组下标的方法叫做 散列函数(或哈希函数), 通过散列函数计算得到的值叫做 散列值(或哈希值) 。
根据下图你更能理解散列表:
树和二叉树
图
「真诚赞赏,手留余香」
真诚赞赏,手留余香
使用微信扫描二维码完成支付
