[TOC]
说明:以下文字来源《大话数据结构》 作者:程杰。
数据和结构的定义
数据
数据是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识别,并输入给计算机处理的符号集合。 也就是说,我们这里说的数据,其实就是符号,而且这些符号必须具备两个前提:
- 可以输入到计算机中。
- 能被计算机程序处理。
相对而言就是一种打的方向描述。
数据元素
是组成数据的,有一定意义的基本单位,在计算机中通常作为整体处理。 也被称为记录。
可以这样理解,数据描述一栋房子,作为一张表,那么这个描述房子的表中的砖头,木材就是基本单位,也就是数据元素。
数据项
一个数据元素可以由若干个数据项组成。 记住了,数据项是数据的最小单位,但真正讨论问题时,,数据元素才是数据结构中建立数据模型的着眼点。
感觉就是一个表中的一条记录的一个特定字段。
数据对象
是性质相同的数据元素的集合,是数据的子集。
什么叫性质相同了? 是指数据元素具有相同数量和类型的数据项。
既然数据对象是数据的子集,在实际应用中,处理的数据元素通常具有相同性质,在不产生混淆的情况下,我们都将数据对象简称为数据。
数据结构
结构,简单的理解就是关系,严格点说,结构是指各个组成部分相互搭配和排序的方式,在现实世界中,不同数据元素之间不是独立的, 而是存在特定的关系,我们将这些关系称为结构。
数据结构:是相互之间存在一种或者多种特定关系的数据元素的集合。
数据结构是是一门眼睛非数值计算的程序设计问题中的操作对象,以及他们之间的关系和操作等相关问题的学科。 人民越来越重视"数据结构",认为程序设计的实质是对确定的问题选择一种好的结构,加上设计一种好的算法。
在计算机中, 数据并是不孤立,杂乱无序的,而是具有内在联系的数据集合。数据元素之间存在的一种或者多种特定关系,也就是数据的组织形式。
逻辑结构与物理结构
按照视点的不同,我们把数据结构分为逻辑结构和物理结构。
逻辑结构
逻辑结构:是指数据对象中数据元素之间的相互关系。
1. 集合结构
集合结构:集合结构中的数据元素除了同属一个集合外,它们之间没有其他的关系。 各个数据是"平等"的,它们的共同属性是"同属于一个集合"。
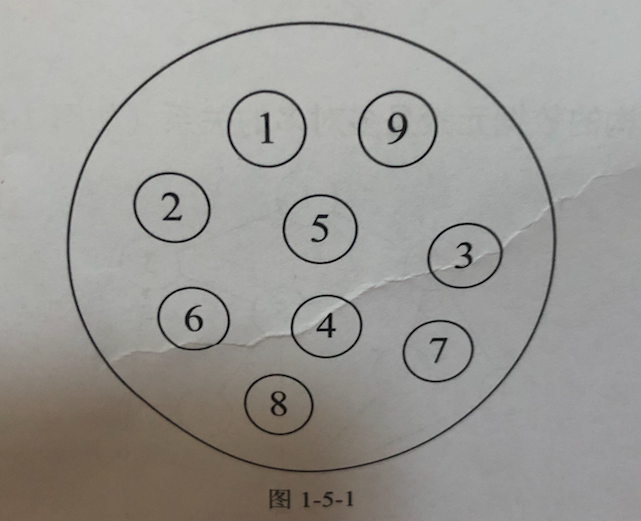
2. 线性结构
线性结构:线性结构中的数据元素之间是一对一的关系。
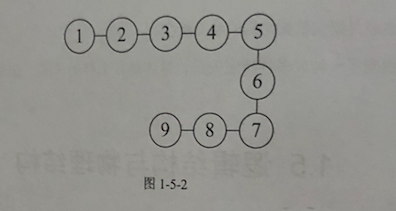
3. 树形结构
树形结构:树形结构中的数据是元素之间存在一种一对多的层次关系。
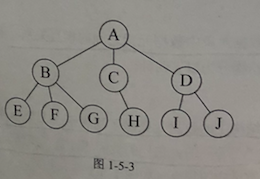
4.图形结构
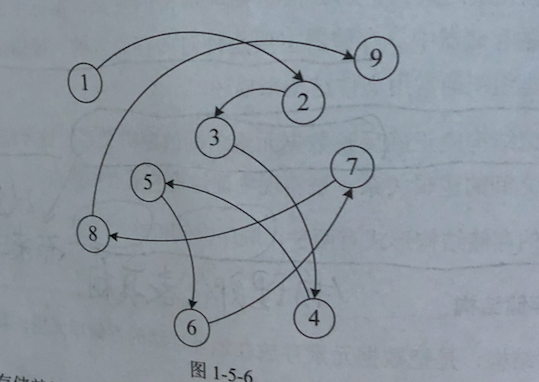
图形结构的数据元素多对多的关系。

总结
逻辑结构是针对具体问题的,是为了解决某个问题在对问题理解的基础上,选择一个合适的数据结构表示数据元素之间的逻辑关系。 逻辑关系更多的事人类的一种用于处理问题的主观思维定义。
物理结构
物理结构:是指数据的逻辑结构在计算机中的存储形式,也就是计算机中的真实的存储形式。
存储器主要是针对内存而言的,像硬盘,软盘,光盘等外部存储器的数据组织通常用文件结构来描述。
数据的存储结构应正确反映数据元素之间的逻辑关系,相当于以逻辑关系为目标,而来实现物理处理。
数据元素的存储结构形式有两种:顺序存储和链式存储。
1. 顺序存储结构
是吧数据元素存放在地址连续的存储单元里,其数据间的逻辑和物理关系是一致的。

数组就是这样的顺序存储结构的。当你告诉计算机,你要建立一个有9个整型数据的数组时,计算机就在内存中找了片空地,按照一个整型所占位置的大小乘以9,开辟 一段连续的空间,于是第一个数组数据就放在第一个位置,第二个数据放在第二,这样依次摆放。
2. 链式存储结构
如果就是这么简单和有规律,一切都好办了。可实际上,总会有人插队,也会有人要上厕所,有人放弃排队。所以这个队伍中会添加新成员,也有可能会去掉老元素,整体的结构都处于变化中。 显然,面对这样的时常要变化的结构,顺序存储是不科学的。那怎么办了?
链式存储结构:是把数据元素放在任意的存储单位里,这组存储单元可以是连续的,也可以是不连续的。**数据元素的存储关系并不能反映其逻辑关系。**因此需要用一个指针存放数据元素的地址,这样通过地址就可以找到相关联数据元素的位置。
总结
逻辑结构是面向问题的,而物理结构是面向计算机的。其基本的目标就是将数据及其逻辑关系存储到计算机的内存中。
算法
什么是算法? 算法是描述解决问题的方法。 算法是解决特定问题求解步骤的描述。在计算机中表现为指令的有序序列,并且每条指令表示一个或者多个操作。
简析时间复杂度和空间复杂度
转载地址:https://blog.csdn.net/haha223545/article/details/93619874
时间复杂度和空间复杂度是用来评价算法效率高低的2个标准,身为开发者肯定会经常会听到这2个概念,但它们分别是什么意思呢?
其实这两个概念从字面意思上也能看出一二:
-
时间复杂度:就是说执行算法需要消耗的时间长短,越快越好。比如你在电脑上打开计算器,如果一个普通的运算要消耗1分钟时间,那谁还会用它呢,还不如自己口算呢。
-
空间复杂度:就是说执行当前算法需要消耗的存储空间大小,也是越少越好。本来计算机的存储资源就是有限的,如果你的算法总是需要耗费很大的存储空间,这样也会给机器带来很大的负担。
时间复杂度
表示方法
我们一般用“大O符号表示法”来表示时间复杂度:T(n) = O(f(n))
n是影响复杂度变化的因子,f(n)是复杂度具体的算法。
常见的时间复杂度量级
- 常数阶O(1)
- 线性阶O(n)
- 对数阶O(logN)
- 线性对数阶O(nlogN)
- 平方阶O(n²)
- 立方阶O(n³)
- K次方阶O(n^k)
- 指数阶(2^n)
接下来再看一下不同的复杂度所对应的算法类型。
log运算符
对数运算符号
log以a为底b的对数 也就5261是让你求a的多少次方等于b 这个多少次方的4102这个数就是这个对数
例子:log2 8(那个2是下角标1653 也就是log以2为底8的对数)=3
意思就是2的3次方等于8
3就是log以2为底8的对数
常数阶O(1)
int a = 1;
int b = 2;
int c = 3;
我们假定每执行一行代码所需要消耗的时间为1个时间单位,那么以上3行代码就消耗了3个时间单位。那是不是这段代码的时间复杂度表示为O(n)呢 ?
其实不是的,因为大O符号表示法并不是用于来真实代表算法的执行时间的,它是用来表示代码执行时间的增长变化趋势的。
上面的算法并没有随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度。
线性阶O(n)
for(i = 1; i <= n; i++) {
j = i;
j++;
}
看这段代码会执行多少次呢? 第1行会执行1次,第2行和第3行会分别执行n次,总的执行时间也就是 2n + 1 次,那它的时间复杂度表示是 O(2n + 1) 吗? No !
还是那句话:“大O符号表示法并不是用于来真实代表算法的执行时间的,它是用来表示代码执行时间的增长变化趋势的”。
所以它的时间复杂度其实是O(n);
对数阶O(logN)
int i = 1;
while(i < n) {
i = i * 2;
}
可以看到每次循环的时候 i 都会乘2,那么总共循环的次数就是log2n,因此这个代码的时间复杂度为O(logn)。 这儿有个问题,为什么明明应该是O(log2n),却要写成O(logn)呢?
其实这里的底数对于研究程序运行效率不重要,写代码时要考虑的是数据规模n对程序运行效率的影响,常数部分则忽略,同样的,如果不同时间复杂度的倍数关系为常数,那也可以近似认为两者为同一量级的时间复杂度。
线性对数阶O(nlogN)
for(m = 1; m < n; m++) {
i = 1;
while(i < n) {
i = i * 2;
}
}
线性对数阶O(nlogN) 其实非常容易理解,将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logN),也就是了O(nlogN)。
平方阶O(n²)
for(x = 1; i <= n; x++){
for(i = 1; i <= n; i++) {
j = i;
j++;
}
}
把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²) 了。
立方阶O(n³)、K次方阶O(n^k)
参考上面的O(n²) 去理解就好了,O(n³)相当于三层n循环,其它的类似。
空间复杂度
空间复杂度 O(1)
如果算法执行所需要的临时空间不随着某个变量n的大小而变化,即此算法空间复杂度为一个常量,可表示为 O(1)。
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
代码中的 i、j、m 所分配的空间都不随着处理数据量变化,因此它的空间复杂度 S(n) = O(1)。
空间复杂度 O(n)
int[] m = new int[n]
for(i = 1; i <= n; ++i) {
j = i;
j++;
}
这段代码中,第一行new了一个数组出来,这个数据占用的大小为n,后面虽然有循环,但没有再分配新的空间,因此,这段代码的空间复杂度主要看第一行即可,即 S(n) = O(n)。
总结
评价一个算法的效率主要是看它的时间复杂度和空间复杂度情况。可能有的开发者接触时间复杂度和空间复杂度的优化不太多(尤其是客户端),但在服务端的应用是比较广泛的,在巨大并发量的情况下,小部分时间复杂度或空间复杂度上的优化都能带来巨大的性能提升,是非常有必要了解的。
在线算法演示
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
「真诚赞赏,手留余香」
真诚赞赏,手留余香
使用微信扫描二维码完成支付
